To illustrate the effect of changing the Gaussian convolution kernel size, I generated a series of 64x64x64 3D noise texture arrays using the code from my 3D MATLAB noise (continued) post:
After the break, see how increasing the size of the convolution kernel affects the quality of the 3D noise.
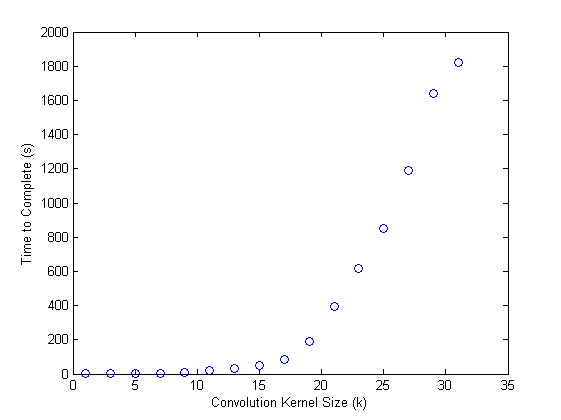
Note that “Time to Process” was calculated tic and toc (see above) on a quad-core Xeon W3530 @ 2.80GHz with 12 GB of RAM. In addition, the 2D FFT animations were generated using each frame of the GIF animations using the following code:
| k | Time to Process | 2D FFT | |
| 1 |  |
0.4167 |  |
| 3 |  |
0.8670 |  |
| 5 |  |
2.2663 |  |
| 7 |  |
5.7784 |  |
| 9 |  |
11.2293 |  |
| 11 |  |
20.8108 |  |
| 13 |  |
33.3277 |  |
| 15 |  |
52.0085 |  |
| 17 |  |
82.3220 |  |
| 19 |  |
187.6235 |  |
| 21 |  |
397.4730 |  |
| 23 |  |
615.1934 |  |
| 25 |  |
852.5891 |  |
| 27 |  |
1190.7 |  |
| 29 |  |
1641.1 |  |
| 31 |  |
1822.3 |  |
Subjectively, there is diminishing return as the convolution kernel increases past 13-15 pixels. Objectively, it makes little sense to spend the computational time processing past 15:
Here is a MAT file with these 3D noise arrays:
noise3Dwrap64_k1_31.mat