The camera included in Google’s Android mobile OS has a feature called “Photo Spheres” that allows you to take a series of photos and create a full spherical panorama. The Photo Sphere feature is included on Google Play Edition (GPE) phones –phones that incorporate Google’s version of unadulterated Android– including my Nexus 5. When you take a Photo Sphere, the camera seamlessly stitches the individual photos into an Equirectangular panorama. For example, here is a panorama I took of the rapeseed fields in central Germany:
There is a bit of distortion (see Tissot’s indicatrix), especially at the top and bottom of the image, but this is due to the problem of projecting a sphere onto a plane. On the Nexus 5 (and other GPE phones), the Gallery application includes a feature that allows you to either view the resulting Photo Spheres as spherical panoramas or to create “Little Planets”/”Tiny Planets”, which are actually Stereographic Projections of the spherical panorama. I found the effect really neat, so I wanted to see if I could recreate the projection in MATLAB.
As a teaser, here’s the output for my code:
Click through to get more information on the MATLAB implementation.
I found some Flash code that performs a similar function to what I wanted to achieve, so I have to send a big thanks to nicoptere for providing his code for PIXEL BENDER #4 projections. Thanks to the examples provided in his code, I was able to translate the projection conversion into MATLAB.
The actual calculation of stereographic projections is well documented on Wolfram Mathworld’s Stereographic Projection page, but basically we only need the last bit dealing with the inverse formulas for latitude 
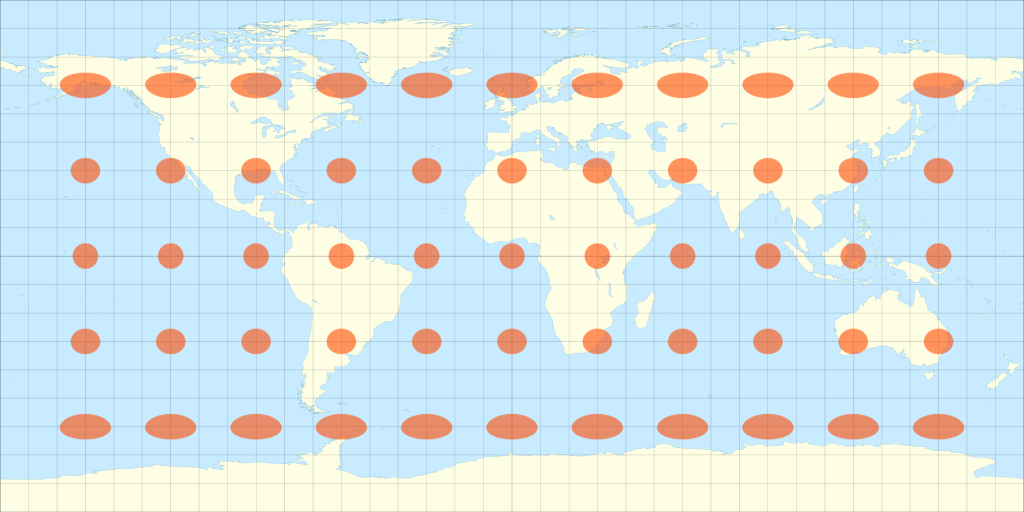
First, just to illustrate how the stereographic projection affects the Tissot’s indicatrix, here is an example based upon a equirectangular world projection from Wikipedia user Eric Gaba (CC BY-SA 3.0):
As you can tell, the output is a function of the latitude and longitude, with the “lowest” latitude in the middle of the image and the “highest” outside the bounds of the projection. This means that Antarctica is in the center while Arctic Circle is not visible.
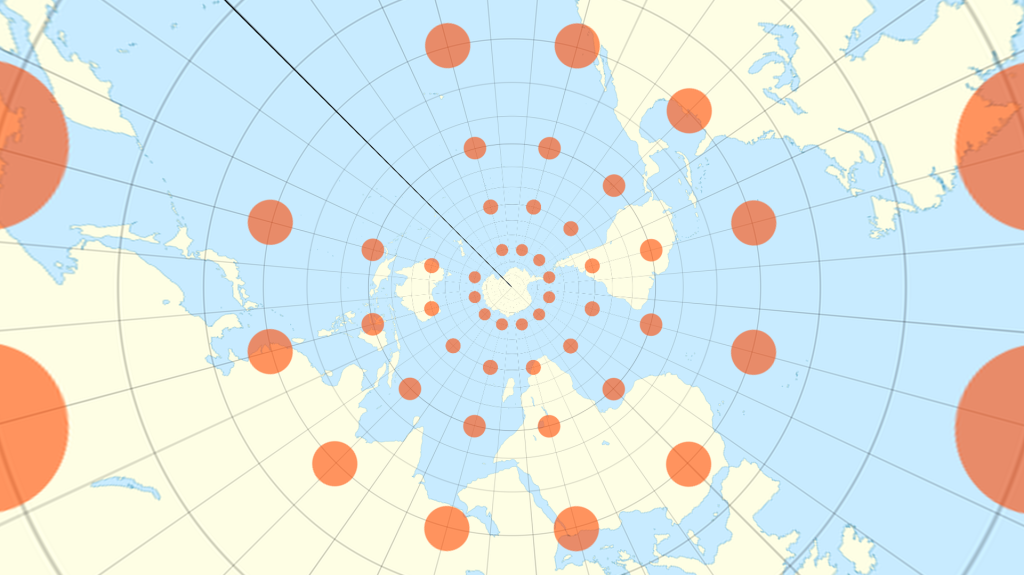
If we apply the equirectangular to stereographic projection function to my image at the top of the post, but sample from the highest latitude for the center of the output image (by inverting the viewing distance in the code below), we can create another visually compelling projection:
For anyone who is interested, here is the function used to generate the equirectangular to stereographic projections (“Little Planets”) in MATLAB. Note that this function requires the inpaint_nans function:
In the statements ‘imresize(outImage,[NaN OUTSIZE(2)]);’and imresize(outImage,[OUTSIZE(1) NaN]); are you sure the ‘NaN’ is right? This can invoke the error ‘Out of memory’.
Hello! I specialize in creating stereographic panorama’s or (“Little Planets”) like the last image posted on this page and I am now wondering if it is possible to generate the stereographic projections (“Little Planets”) to an equirectangular panorama for building virtual tours. “Part of the complication is that I have photoshopped the panorama’s and they are now 1 flat image, not multiple pictures/layers.” This conversion seems to be the exact opposite of what everyone else is trying to do so I haven’t had much luck with figuring this out. Please help! Thanks!!
Hello, I could’n find any post as you said to get you source codes, could you please give me the link? Thanks!